
I originally planned to write a post on d3. I also originally planned to write it two weeks ago. However, due to rEaSoNs my priorities have suddenly shifted and all my time is now spent studying data structures and algorithms.
This was a rough cold-start. I might describe my Code Bootcamp’s teaching on the subject as either “introductory” or “compressed”. I don’t remember much from college, other than the professor failed half of the class (not including myself) for cheating off each other’s homework and it was A Whole Big Thing.
A surprising moment the other day was encountering the Trie data structure. It was never taught in college, or if it was, it wasn’t worth copying anybody’s homework over and I don’t remember it. Cracking The Coding Interview dedicates a little under a single page to it. There are plenty of Youtube overviews, but they are just that — high-level, introductory overviews on weirdly-lit whiteboards.
For what is supposedly a niche data structure, Tries sure seem to come up on coding interviews A LOT. I asked around my friends and almost everybody has encountered one on a whiteboarding interview. It’s funny, because they’re supposedly so uncommon in the real world.
Fun fact: one of the few real world, actual uses for Tries is in NLP development and libraries.
I had a hard time finding good information on implementing a Trie, especially in Javascript, so here we go.
Reading is Boring
What is a Trie?
Usually, people say a Trie is a tree specialized for strings.
I think this is too specific a definition. Yes, most of the Tries in the world exist solely for string prefix questions on whiteboards or Leetcode, but real-world Tries can operate on entire phrases or other types of data.
I would prefer to define a Trie as:
A tree specialized for storing and searching chains of values that are only valid if all values in the chain are present.
Another couple different ways to put it:
- Tries are trees optimized for DFS
- Tries are trees optimized for insertion
An Illustration and Some Observations
Here’s an illustration of a Trie. This Trie contains the following words:
- ale
- alex
- he
- hen
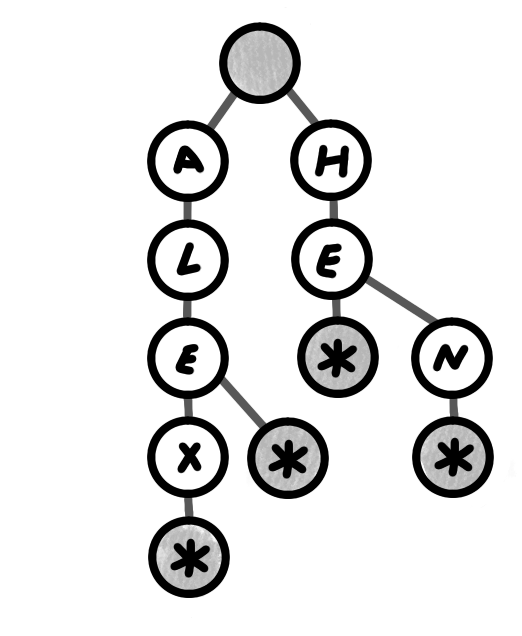
Some things to observe
- Tries are generally NOT binary. However, nothing is impossible and some chaotic evil algorithm question probably exists out there that requires the implementation of a binary Trie.
- The root is empty, or has no value
- Each leaf is a node with a value * This doesn’t represent the literal value on the node; most diagrams just use this convention. What it does represent is that the node has some property to indicate it is the end of a valid chain of values.
- Duplicate values occur. The letters e and x appear in several subtrees, but they are duplicate values on different nodes, and their children are not shared
Making a Trie
Types First
Tries extend all the properties of a Tree; each node is in turn a Tree.
A trie node is sometimes defined as having a value property, and sometimes not. I’ve seen both of the below used for implementations:
interface Trie {
children: { [key: string]: Trie };
isWord: boolean;
}or
interface Trie {
value: string;
children: { [key: string]: Trie };
isWord: boolean;
}I prefer to omit the value property to be concise, because it is not needed. On the other hand, it has better usefulness in implementing a remove method.
The isWord property can be set true to represent the end of a valid chain. This is what the * nodes in the above diagram refer to.
Insertion
Inserting a word or chain of values means simply checking if there is a child node that corresponds to each value, adding it if not, and then moving down the chain. Be sure to mark the last node as being the valid termination.
function insert(trie: Trie, word: string) {
let currentNode: Trie = trie;
//traverse down the tree, adding each letter as a child if needed
for (let i = 0; i < word.length; i++) {
let character = word[i];
//if the node doesn't have this current letter in its children...
if (!currentNode.children[character]) {
//add the current letter as a key, and a new node as the value
currentNode.children[character] = {
isWord: false,
children:
;
}
//set the current node to the next node in the chain
currentNode = currentNode.children[character];
}
currentNode.isWord = true; //mark the end!
return word; //or whatever, I don't care what you return
}Insertion Complexity
This is where the DFS optimization comes in; the lookup for a child at each node is constant time. Thus we are O(w) where w is the number of values in the inserted chain (letters in the word, etc).
Search or containsWord
Similar to insertion, but instead we’re only checking if each value exists. Same as insert, we only loop for the number of values in the chain, giving us a O(w) runtime where w is the number of letters in the search term.
function containsWord(trie: Trie, word: string) {
let currentNode: Trie = trie;
for (let i = 0; i < word.length; i++) {
let character = word[i];
if (!currentNode.children[character]) {
return false;
}
}
return currentNode.isWord;
}Remove word
This is the harder one. You must:
- Traverse down the tree to the end of the word/chain, and remove the isWord marker from the last node.
- Move back up the tree and trim off any nodes without other children
I implemented this by pushing each node onto a stack on the way down in step 1. For step 2, you can then move back up the tree by popping nodes from the stack and following a couple of rules for each case.
function remove(trie: Trie, word: string) {
let currentNode: Trie = trie;
let stack: Trie[] = [];
for (let i = 0; i < word.length; i++) {
let character = word[i];
if (!currentNode.children[character]) {
return false; //word isn't in tree; return false
}
stack.push(currentNode);
currentNode = currentNode.children[character];
}
currentNode.isWord = false;
//if there are other children (and thus words) stemming from this node, return
if (Object.keys(currentNode.children).length) {
return true;
}
//else, retrieve the parent
while (stack.length) {
let parent: Trie | undefined = stack.pop();
//if the parent has only one child, that child is the current node, so we can remove all children
if (Object.keys(parent.children).length === 1) {
parent.children = {};
//if the parent represents the end of another word, don't trim upwards anymore
if (parent.isWord) {
return;
}
}
//if there are multiple children for the parent, we search for this currentNode and remove it
for (let child in parent.children) {
if (parent.children[child] === currentNode) {
//remove by setting the value for the key to empty Trie
parent.children[child] = { isWord: false, children:
}
currentNode = parent;
}
return true;
}Remove Complexity
On the way down: W loops, 1 for each letter in the word, so O(w)
On the way back up (trimming): We run the while loop for each item in the stack, exiting early under certain conditions. Worst case is if the removed word was the only one on the chain, so we must see W loops. This gives O(w + w) or O(w) complexity.